High Impact
Experimentation
24
Faculty members who research condensed matter, particle physics, biophysics, and astrophysics and cosmology
#1
UCSC Physics’ professional papers had the highest citation rate of any physics department in the country
2
International Congress of Basic Science (ICBS) honors two UC Santa Cruz physicists with Frontiers of Science Award
Quantum to the Cosmos – Physics at UC Santa Cruz
Our department pushes the frontiers of knowledge across theory, experiment, and computation. From unraveling quantum mysteries to probing the structure of the universe, we prepare students to lead in science and beyond.
Welcome
We are a vibrant community of researchers, educators, and students exploring the fundamental laws of nature – from the smallest quantum particles to the largest structures in the universe. Whether you’re an aspiring physicist or a curious visitor, we invite you to discover the groundbreaking research, dynamic teaching, and collaborative spirit that define Physics at UC Santa Cruz.
Department Events
Explore our department calendar and check out the various events we have! Join us for our weekly Condensed Matter Seminar and Colloquium. Get the chance to hear from experts in the field from universities all over the world, including here at UC Santa Cruz!
Undergraduate
Programs
Graduate
Programs
Physics News

Global physics conference comes to UC Santa Cruz for first time—and why it matters
Physicists from around the world will converge on campus to offer possible answers to some of the biggest and most vexing questions about the particle makeup of the universe and everything in it.
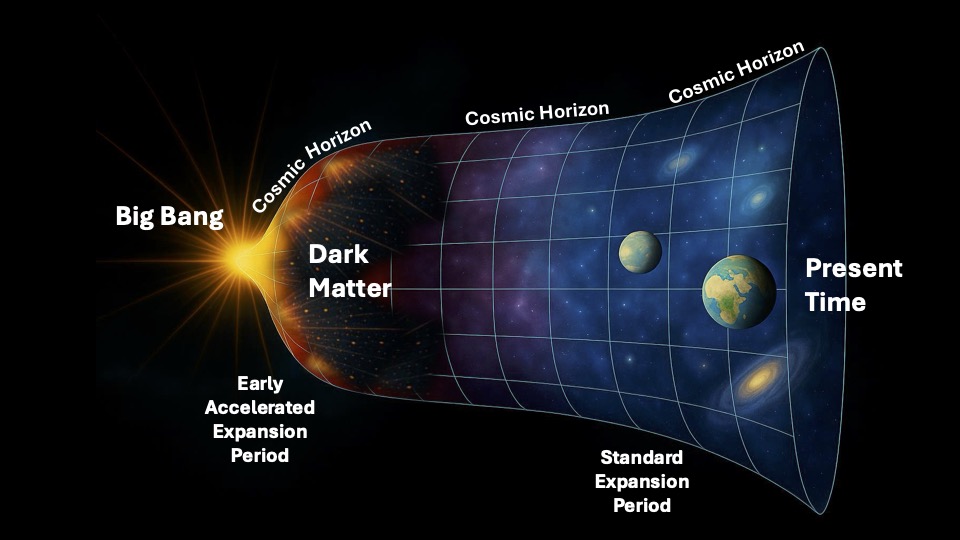
New theories on dark matter’s origins point to ‘mirror world’ and universe’s edge
Two recent studies speculate a natural emergence of the mysterious substance, offering ‘self-contained and calculable scenarios’

The Science Division announces recipients of Distinguished Alumni Awards
Gabriel Filippelli, Aradhna Tripati, and Seath Brook Ahrens are this year’s Distinguished Alumni Award recipients for the Science Division

Meet the faculty
The Physics Department is made up of twenty-four faculty members, who conduct research in the areas of condensed matter (theory and experiment), particle physics (theory and experiment), biophysics, and astrophysics and cosmology. We are home to some of the most creative faculty and unique research programs in the nation. As individuals, our faculty members have received numerous awards.
View directory
Support Us
Throughout its history, the Physics Department at UC Santa Cruz has relied on the generosity of its alumni and friends. Never before has private support been so important. Your gift is an investment that will allow us to enrich and enhance our programs.